8. sınıf Kareköklü Sayılarla Çarpma Bölme|KONU ANLATIMI|NEDİR|NASILDIR|4|5|6|7|8|9|10|11|12|SINIF|RESİMLİ|VİDEOLU|SORULARI|ÇÖZÜMLERİ|
8. sınıf Kareköklü Sayılarla Çarpma Bölme Konu Anlatımı Video Çözümlü Soruları Testleri Çöz izle indir
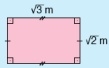Kenar uzunlukları m ve m olan dikdörtgeni ele alalım. Bu dikdörtgenin alanını bulunuz. Nasıl bulduğunuzu açıklayınız. Kareköklü sayılarla çarpma işlemiyle ilgili bir kural geliştirebilir misiniz? Tartışınız. Kareköklü sayılar çarpılırken (varsa) katsayılar çarpılarak çarpıma katsayı olarak yazılır. Kareköklü iki sayı ise tek bir karekök içine yazılarak çarpılır ve çarpıma yazılır.
Kareköklü Sayılarda Bölme İşlemi
Yandaki örüntünün ilk üç satırını inceleyelim. Kareköklü sayılarla bölme işleminin nasıl yapıldığını açıklayınız. Yandaki örüntünün 4. satırındaki ondalık kesrin karekökünü ele alalım. Ondalık kesri, kesir sayısı olarak nasıl ifade edersiniz? Açıklayınız. Kesir sayısı olarak ifade ettiğiniz ondalık kesrin karekökünü nasıl bulacağınızı tartışınız.
1) Aşağıdaki işlemleri yaparak en sade biçimde yazınız.
a) 3( √5 + √2 ) b) 3 ( √3 - √5 ) c) 5 ( √2 -√ 3 ) ç) 5 ( √2 +√ 3 )
2) √35 sayısını iki kareköklü sayısının çarpımı şeklinde yazınız.
Kenar uzunlukları m ve m olan dikdörtgeni ele alalım. Bu dikdörtgenin alanını bulunuz. Nasıl bulduğunuzu açıklayınız. Kareköklü sayılarla çarpma işlemiyle ilgili bir kural geliştirebilir misiniz? Tartışınız. Kareköklü sayılar çarpılırken (varsa) katsayılar çarpılarak çarpıma katsayı olarak yazılır. Kareköklü iki sayı ise tek bir karekök içine yazılarak çarpılır ve çarpıma yazılır.Kareköklü Sayılarda Bölme İşlemi
Yandaki örüntünün ilk üç satırını inceleyelim. Kareköklü sayılarla bölme işleminin nasıl yapıldığını açıklayınız. Yandaki örüntünün 4. satırındaki ondalık kesrin karekökünü ele alalım. Ondalık kesri, kesir sayısı olarak nasıl ifade edersiniz? Açıklayınız. Kesir sayısı olarak ifade ettiğiniz ondalık kesrin karekökünü nasıl bulacağınızı tartışınız.
1) Aşağıdaki işlemleri yaparak en sade biçimde yazınız.
a) 3( √5 + √2 ) b) 3 ( √3 - √5 ) c) 5 ( √2 -√ 3 ) ç) 5 ( √2 +√ 3 )
2) √35 sayısını iki kareköklü sayısının çarpımı şeklinde yazınız.